Thinking About Spacetime Symmetries in Field Theory

Published September 01, 2024

In physics, fields are thought of as functions on spacetime that carry indices which determine how they transform under symmetries. But a cleaner, more satisfying way to think about fields is to think differential geometrically — of spacetime as a differentiable manifold, fields as sections of vector bundles, and spacetime symmetries as a group action on spacetime. From this point of view, the action of a symmetry group on the space of fields is determined by underlying geometric structures, and once the correct geometric structure is identified, this action can be deduced by appeals to “naturality”¹.

Let \(M\) be the spacetime manifold, and for the purposes of this post, let the group of diffeomorphisms, \(\mathrm{Diff}(M)\), be the group of spacetime symmetries². As warm up let us think about scalar fields that are just functions on \(M\), i.e., sections of the trivial line bundle. The only natural way a diffeomorphism \(\Lambda : M \to M\) can act on this scalar field, \(\phi : M \to \mathbb R\), is by pulling it back by \(\Lambda^{-1}\),

which is precisely how physics textbooks³ write the transformation rule for scalar fields. Let us see what happens in a nontrivial example.

Vector Fields

Vector fields are sections of the tangent bundle \(TM \to M\). Diffeomorphisms act on vector fields in a natural way by pushforwards. In particular, for a vector field \(v\), and a diffeomorphism \(\Lambda\), the action is given by

where \(\Lambda_\ast\) is the pushforward of vector fields induced by \(\Lambda\). Once again, this can be identified as the familiar transformation law for vector fields from physics textbooks.

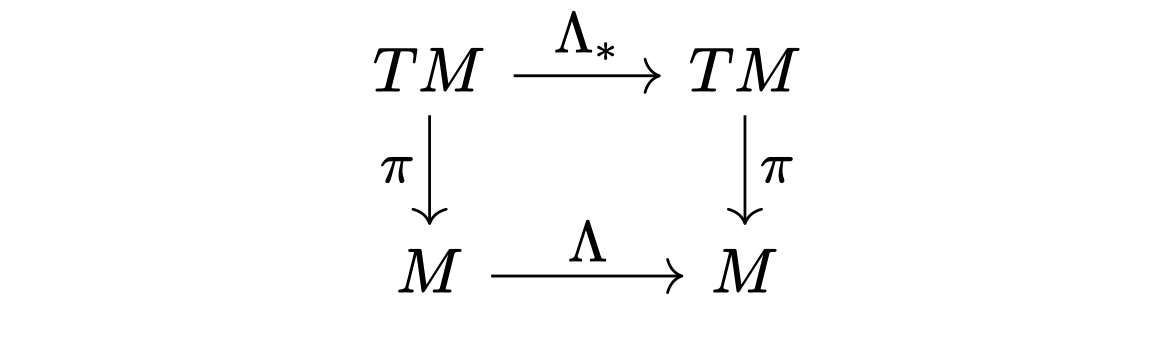
However, note that the pushforward — seen as a bundle map — does two distinct things: (1) moves fibers around, and (2) acts on fibers by a linear transformation. How precisely these two decouple, is the content of the universal property of pullback bundles.

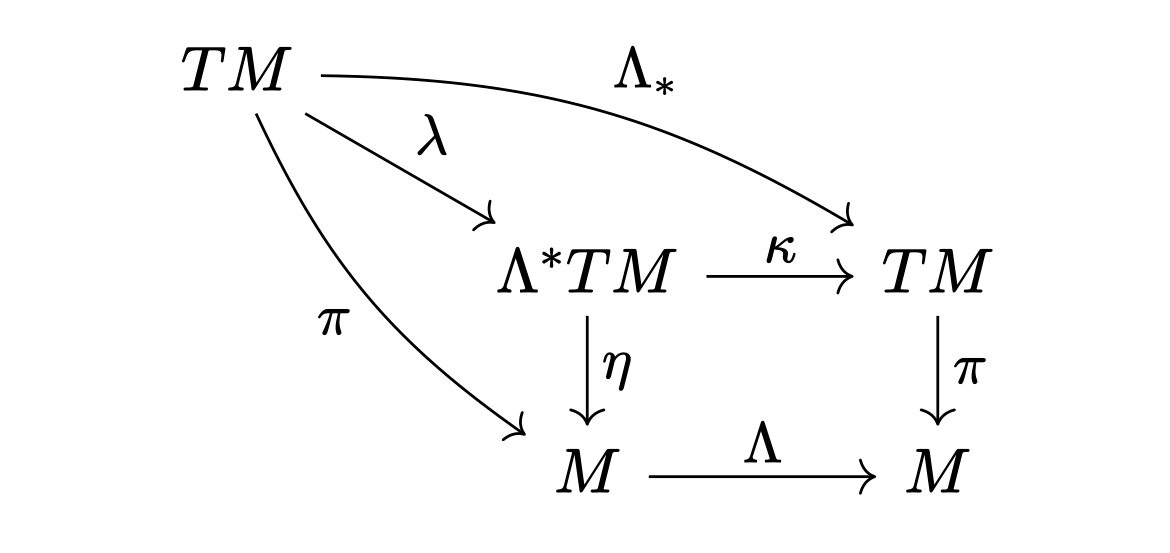
Per this universal property, the bundle map \(\Lambda_\ast = \kappa \circ \lambda\) factors through the pullback bundle \(\Lambda^\ast TM \cong TM\), by a unique map \(\lambda\). If \(v\) is a vector field, then the action of \(\kappa\) is to move the fiber around, i.e., \((\kappa\cdot v)(p) = v(\Lambda^{-1} p)\). And the action of \(\lambda\) is a linear transformation of fibers \((\lambda \cdot v)(p) = \lambda(p) v(p)\), where \(\lambda(p) \in \mathrm{GL}(T_p M)\).

Before moving to more generic situations, it is nice to pause and note that the transformation rule for scalar fields I wrote in the introduction, is a special case of what happens to vector fields. Fibers are moved around but the action on fibers is trivial.

If you are eagle-eyed (or if you already know where this story is going), you may ask if the bundle automorphism \(\lambda\) has an interpretation as a section of some bundle over \(M\) whose fibers are the group \(\mathrm{GL}(\mathbb{R}^m)\). This is correct and the interpretation is fleshed out in the following paragraphs.

To understand more general kinds of fields, we should look for a geometric structure that unifies and generalizes the examples above. This geometric structure is that of a principal \(G\)-bundle and associated vector bundles.

Principal Bundles

A principal \(\mathrm{SO}(m)\)-bundle that comes for free with every orientable manifold is the bundle of oriented orthonormal frames of the tangent bundle⁴, which I will denote \(\mathrm{SO}(M) \to M\). An almost tautological remark is that the tangent bundle is isomorphic to the associated bundle \(\mathrm{SO}(M) \times_\mathbf{m} \mathbb{R}^m\), where \(\mathbf{m}\) is the defining representation of \(\mathrm{SO}(m)\). Real scalar fields can be seen as sections of the associated line bundle \(\mathrm{SO}(M) \times_\mathbf{1} \mathbb{R}\), where \(\mathbf{1}\) is a one-dimensional real representation of \(\mathrm{SO}(m)\).

An abstract but more geometric way of thinking about vector bundles is to regard the associated frame bundle — a principal \(G\)-bundle for an appropriate structure group \(G\) — as the basic object, which gives rise to a whole family of vector bundles with the same topology⁵, indexed by linear representations of \(G\). From this point of view, we can construct a large class of fields on \(M\), as sections of \(\mathrm{SO}(M) \times_\rho V\) for every representation \(\rho : \mathrm{SO}(m) \to \mathrm{GL}(V)\).

To see how diffeomorphisms act on these fields we can run parallel to the discussion above on vector fields, once we note that vector bundle maps induce maps of associated frame bundles. So, a diffeomorphism induces the principal bundle map

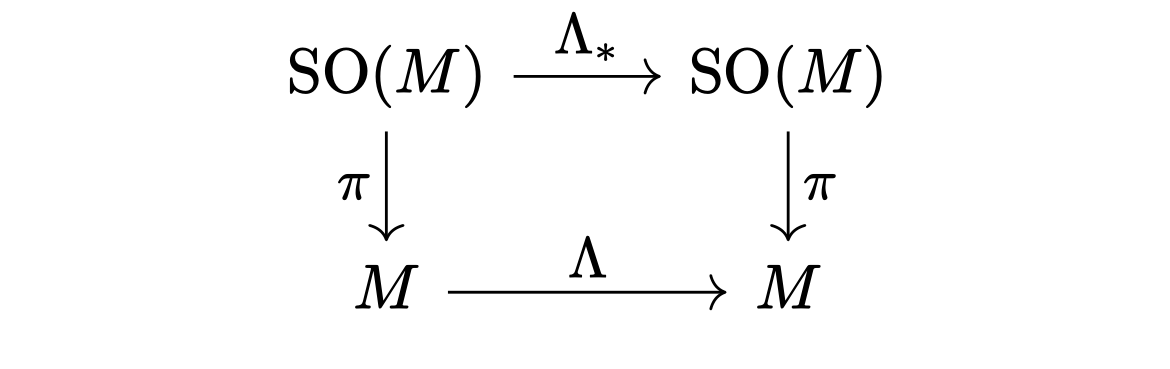
which factors uniquely through the pullback bundle, \(\Lambda^\ast \mathrm{SO}(M) \cong \mathrm{SO}(M)\) as

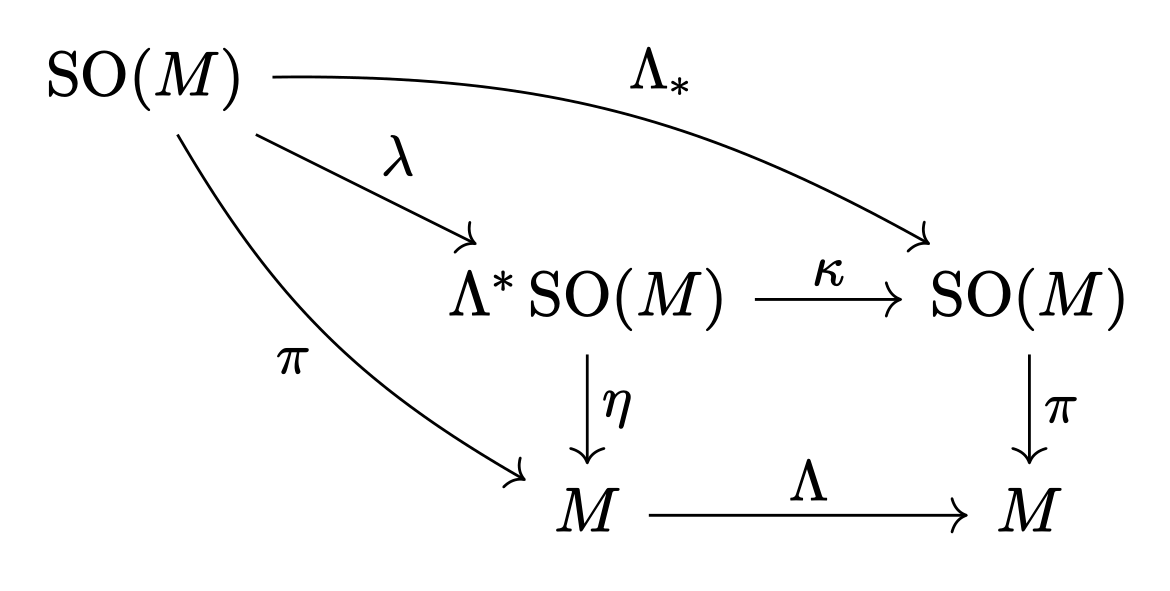
As before \(\kappa\) moves fibers around, and \(\lambda\) acts on the fibers as a bundle automorphism⁶. Principal bundle automorphisms are sections of the adjoint bundle, so \(\lambda\) is a section of the associated bundle \(\mathrm{SO}(M) \times_\textrm{Ad} \mathrm{SO}(m)\).

On sections, \(\varphi\), of the associated vector bundle \(\mathrm{SO}(M) \times_\rho V\), a diffeomorphism acts as a composition of a coordinate change \(\kappa\), and a bundle automorphism \(\lambda\) as follows

where \((\lambda \cdot \varphi)(p) = \rho(\lambda(p))\varphi(p)\).

The upshot of all this abstract⁷ language is that the action of spacetime symmetries on any field that you can possibly think of is either — in case of tensors — a special case of the formula above, or — for spinors or superfields — a straightforward generalization of it. To wrap up, I will sketch how \(\mathrm{Diff}(M)\) acts on tensor fields and spinors.

An \((a, b)\)-tensor field on \(M\) is a section of the vector bundle \(TM^{\otimes a} \otimes T^\ast M^{\otimes b}\). Or in the language of principal bundles, it is a section of the vector bundle associated to \(\mathrm{SO}(M)\) with \(\rho = \mathbf{m}^{\otimes a} \otimes \mathbf{\bar m}^{\otimes b}\), where \(\mathbf m\) is the fundamental representation of \(SO(m)\) and \(\mathbf{\bar m}\) is its dual. In local coordinates, \(\rho(\lambda)\) will become the famous transformation rule for tensors.

Finally, if the spacetime manifold supports a spin structure then spinor fields can be understood as sections of an associated spinor bundle. In particular, given a choice of spin structure on \(M\), there is a principal \(\mathrm{Spin}(m)\)-bundle over it, \(\mathrm{Spin}(M) \to M\). Dirac spinor fields on \(M\) are sections of the associated vector bundle \(\mathrm{Spin}(M) \times_\sigma \Delta_m\), where \(\sigma : \mathrm{Spin}(m) \to \mathrm{GL}(\Delta_m)\) is a particular complex representation of the spin group called the spinor representation.

To see how a diffeomorphisms acts on a spinor fields, note that — modulo some assumptions on the topology of \(M\) — the \(\mathrm{SO}(M)\) bundle map induced by a diffeomorphism lifts to a \(\mathrm{Spin}(M)\) bundle map. As before, this bundle map can be decomposed, via the pullback bundle, into a piece that moves the fiber around and a piece that acts on fibers. So that the transformation rule for spinors can be written as

where the bundle automorphism, \(\lambda : \mathrm{Spin}(M) \to \mathrm{Spin}(M)\), acts on each fiber by the spinor representation \((\lambda \cdot \psi)(p) = \sigma(\lambda(p)) \psi(p)\).